-
For each of the following implementations
derive an expression for the total memory space required
to represent a set which contains of n elements
drawn from the universe
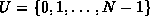 .
.
- SetAsArray (Program
 ),
), - SetAsBitVector (Program
 ),
), - MultisetAsArray (Program
 ), and
), and - MultisetAsLinkedList (Program
 ).
).
-
In addition to = and
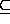 ,
a complete repertoire of set operators includes
,
a complete repertoire of set operators includes
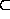 ,
, 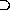 ,
, 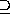 and
and 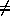 .
For each of the set implementations listed in Exercise
.
For each of the set implementations listed in Exercise  show how to implement the remaining operators.
show how to implement the remaining operators. -
The symmetric difference of two sets S and T,
written
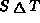 is given by
is given by
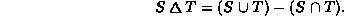
For each of the set implementations listed in Exercise  devise an algorithm to compute symmetric difference.
What is the running time of your algorithm?
devise an algorithm to compute symmetric difference.
What is the running time of your algorithm?
-
The complement
of a set S over universe U,
written S' is given by

Devise an algorithm to compute the complement of
a set represented as a bit vector.
What is the running time of your algorithm?
-
Devise an algorithm to sort a list of integers using a multiset.
What is the running time of your algorithm?
Hint: See Section
 .
. -
Consider a multiset implemented using linked lists.
When the multiset contains duplicate items,
each of those items occupies a separate list element.
An alternative is to use a linked list of ordered pairs
of the form
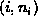 where i an the element of the universal set U
and
where i an the element of the universal set U
and 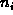 is a non-negative integer that counts the number
of instances of the element i in the multiset.
is a non-negative integer that counts the number
of instances of the element i in the multiset.
Derive an expression for the total memory space required
to represent a multiset which contains of n instances
of m distinct element drawn from the universe 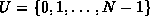 .
.
-
Consider a multiset implemented
as described in Exercise
 .
Devise algorithms for set union, intersection, and difference.
What are the running times of your algorithms?
.
Devise algorithms for set union, intersection, and difference.
What are the running times of your algorithms? -
Consider the initial partition
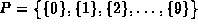 .
For each of the methods of computing the union listed below
show the result of the following sequence join operations:
.
For each of the methods of computing the union listed below
show the result of the following sequence join operations:
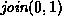 ,
,
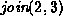 ,
,
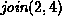 ,
,
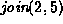 ,
,
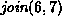 ,
,
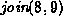 ,
,
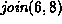 ,
,
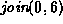 ,
,
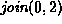 .
.
- simple union,
- union by size,
- union by height, and
- union by rank.
-
For each final partition obtained in Exercise
 ,
show the result of performing a collapsing find
operation for item 9.
,
show the result of performing a collapsing find
operation for item 9. -
Consider the initial partition P
of the universe
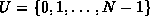 comprised of N sets[22].
comprised of N sets[22].
-
Show that N-1 join operations can be performed
before the number of elements in the partition
is reduced to one.
-
Show that if n join operations are done (
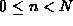 ),
the size of the largest element of the partition is
at most n+1.
),
the size of the largest element of the partition is
at most n+1. -
A singleton
is an element of a partition
that contains only one element of the universal set.
Show that when n join operations are done (
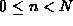 ),
at least
),
at least 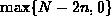 singletons are left.
singletons are left. -
Show that if less that
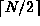 join operations
are done,
at least one singleton is left.
join operations
are done,
at least one singleton is left.
![]()
![]() devise an algorithm to compute symmetric difference.
What is the running time of your algorithm?
devise an algorithm to compute symmetric difference.
What is the running time of your algorithm?![]()
![]() .
.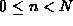 ),
the size of the largest element of the partition is
at most n+1.
),
the size of the largest element of the partition is
at most n+1.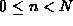 ),
at least
),
at least 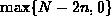 singletons are left.
singletons are left.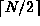 join operations
are done,
at least one singleton is left.
join operations
are done,
at least one singleton is left.