Data Structures and Algorithms
with Object-Oriented Design Patterns in Java 
In this example we consider the problem of computing a
geometric series summation
for the last time.
We have already seen two algorithms to compute this summation
in Sections 
and
(Programs and ).
An algorithm to compute a geometric series summation
using the closed-form expression (Equation )
is given in Program .
This algorithm makes use of Program to compute 
.
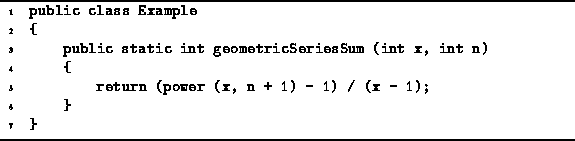
Program: Program to compute 
using the closed-form expression.
To determine the average running time of Program
we will make use of Equation ,
which gives the average running time for the power method
which is called on line 5.
In this case, the arguments are x and n+1,
so the running time of the call to power is
.
Adding to this the additional work done on line 5 gives
the average running time for Program :
The running times of the three programs
which compute the geometric series summation
presented in this chapter are tabulated below
in Table
and are plotted for 
in Figure .
The plot shows that,
according to our simplified model of the computer,
Program has the best running time for n<4.
However as n increases,
Program is clearly the fastest of the three
and Program is the slowest for all values of n.
| program | T(n) |
| Program |  |
|
Program | 13n+22 |
|
Program |  |
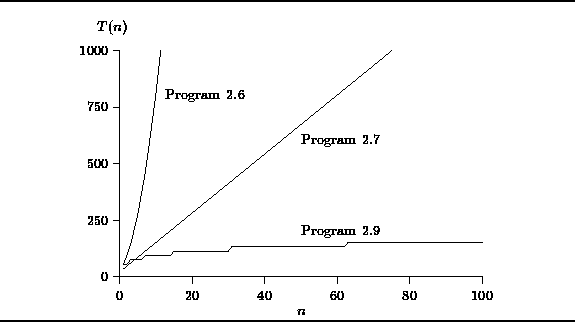
Figure: Plot of running time vs. n for Programs , and .
Copyright © 1998 by Bruno R. Preiss, P.Eng. All rights reserved.