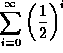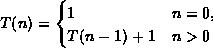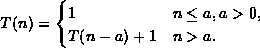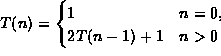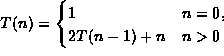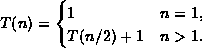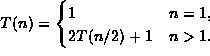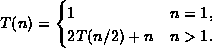-
for (int i = 0; i < n; ++i) ++k; -
for (int i = 1; i < n; i *= 2) ++k; -
for (int i = n - 1; i != 0; i /= 2) ++k; -
for (int i = 0; i < n; ++i) if (i % 2 == 0) ++k; -
for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) ++k; -
for (int i = 0; i < n; ++i) for (int j = i; j < n; ++j) ++k; -
for (int i = 0; i < n; ++i) for (int j = 0; j < i * i; ++j) ++k;