Forward-Backwards Filtering

One is normally told there is no such thing as a linear phase recursive filter because a recursive filter cannot generate a symmetric impulse response. However, it is possible to implement recursive, zero-phase filters offline. That is, if the entire input signal $x(\cdot)$ is stored on a computer disk, e.g., we can apply a recursive filter both forwards and backwards in time. Doing this squares the amplitude response of the filter and zeros the phase response.

To show this analytically, let $v(n)$ denote the output of the first filtering operation (which we'll take to be ``forward'' in time in the normal way), and let $h(n)$ be the impulse response of the recursive filter. Then we have

$$v(n) = (h\ast x)(n)$$

where $x(n)$ is the input signal at sample $n$. For the second pass, we ``flip'' $v(n)$ to obtain $v(-n)$ and apply the filter again:

$$w(n) = (h\ast$$   FLIP$$(v))(n)$$

The final output is then this result flipped:

$$y =$$   FLIP$$(w) =$$   FLIP$$(h\ast$$   FLIP$$(v)) =$$   FLIP$$(h)\ast v$$

where the last simplification tells us that flipping the input and output signals is equivalent to flipping the impulse response instead. Putting all these operations together, we have

$$y(n) =$$   FLIP$$_n(h\ast$$   FLIP$$(h\ast x)) = ($$FLIP$$(h)\ast (h\ast x))(n)$$

By the flip theorem for z transforms, we have that the z transform of FLIP$(x)$ is $X(z^{-1})$:

$$\begin{eqnarray*} {\cal Z}\{\mbox{{\sc Flip}}(x)\} &\isdef & \sum_{n=-\infty}^\i... ... &=& \sum_{m=-\infty}^\infty x(m) (z^{-1})^{-m} \isdef X(z^{-1}) \end{eqnarray*}$$

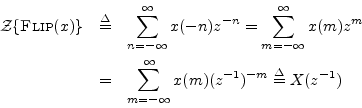
Using this result and applying the convolution theorem twice gives the z transform

$$Y(z) = H(z^{-1})[H(z)X(z)].$$

On the unit circle, this reduces to, for real filters $h$,

$$\begin{eqnarray*} Y(e^{j\omega T}) &=& H(e^{-j\omega T})H(e^{j\omega T})X(e^{j\o... ...rt^2 X(e^{j\omega T})\\ &\isdef & G^2(\omega) X(e^{j\omega T}). \end{eqnarray*}$$

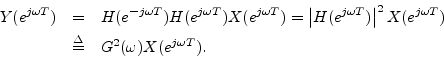
We have thus shown that forwards-backwards filtering squares the amplitude response and zeros the phase response. Note also that the phase response is truly zero, not alternating between zero and $\pi$.

In summary, no matter what nonlinear phase response $\Theta(\omega)$ a filter may have, this phase is completely canceled out by forward and backwards filtering. The amplitude response, on the other hand, is squared. For simple bandpass filters (including lowpass, highpass, etc.), for which the desired gain is 1 in the passband and 0 in the stopband, squaring the amplitude response usually improves the response, however, since any ``stopband ripple'' (deviation from 0) is squared, thereby doubling the stopband attenuation in dB. On the other hand, passband ripple (deviation from 1) is only doubled by the squaring (since $(1+\epsilon)^2 = 1+2\epsilon + \epsilon^2\approx 1+2\epsilon$).

A Matlab example of forward-backward filtering is presented in §12.3 (Fig.12.1).