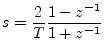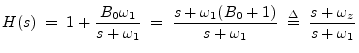
The analog transfer function for a low shelf is given by [102,6]
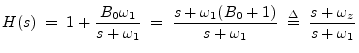
A high shelf is obtained from a low shelf by the conformal mapping
![]() , which interchanges high and low frequencies, i.e.,
, which interchanges high and low frequencies, i.e.,
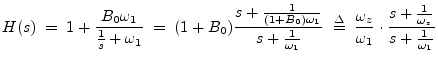
To convert these analog-filter transfer functions to digital form, we apply the bilinear transform: