Transfer Function Analysis

This chapter discusses filter transfer functions and associated analysis. The transfer function provides an algebraic representation of a linear, time-invariant (LTI) filter in the frequency domain:

$\parbox{0.8\textwidth}{The \emph{transfer function}\index{transfer f... ..., and $X(z)$\ denotes the {\it z} transform of the filter input signal $x(n)$.}$

The transfer function is also called the system function [60].

Let $h(n)$ denote the impulse response of the filter. It turns out (as we will show) that the transfer function is equal to the z transform of the impulse response $h(n)$:

$$\zbox {H(z) = \frac{Y(z)}{X(z)}}$$

Since multiplying the input transform $X(z)$ by the transfer function $H(z)$ gives the output transform $Y(z)$, we see that $H(z)$ embodies the transfer characteristics of the filter--hence the name.

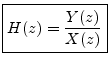
It remains to define ``z transform'', and to prove that the z transform of the impulse response always gives the transfer function, which we will do by proving the convolution theorem for z transforms.