Choose any two complex numbers ![]() and
and ![]() , and form the sequence
, and form the sequence
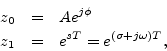
we see that the signal ![]() is always a discrete-time
generalized (exponentially enveloped) complex sinusoid:
is always a discrete-time
generalized (exponentially enveloped) complex sinusoid:
Figure 4.17 shows a plot of a generalized (exponentially
decaying, ![]() ) complex sinusoid versus time.
) complex sinusoid versus time.
Note that the left projection (onto the ![]() plane) is a decaying spiral,
the lower projection (real-part vs. time) is an exponentially decaying
cosine, and the upper projection (imaginary-part vs. time) is an
exponentially enveloped sine wave.
plane) is a decaying spiral,
the lower projection (real-part vs. time) is an exponentially decaying
cosine, and the upper projection (imaginary-part vs. time) is an
exponentially enveloped sine wave.