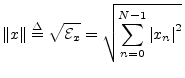Signal Metrics

This section defines some useful functions of signals (vectors).

The mean of a signal $x$ (more precisely the ``sample mean'') is defined as the average value of its samples:^5.5

$$\mu_x \isdef \frac{1}{N}\sum_{n=0}^{N-1}x_n$$   $$\mbox{(mean of $x$)}$$

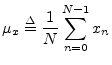
The total energy of a signal $x$ is defined as the sum of squared moduli:

$${\cal E}_x \isdef \sum_{n=0}^{N-1}\left\vert x_n\right\vert^2$$   $$\mbox{(energy of $x$)}$$

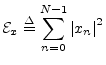
In physics, energy (the ``ability to do work'') and work are in units of ``force times distance,'' ``mass times velocity squared,'' or other equivalent combinations of units.<sup>5.6</sup> In digital signal processing, physical units are routinely discarded, and signals are renormalized whenever convenient. Therefore, ${\cal E}_x$ is defined above without regard for constant scale factors such as ``wave impedance'' or the sampling interval $T$.

The average power of a signal $x$ is defined as the energy per sample:

$${\cal P}_x \isdef \frac{{\cal E}_x}{N} = \frac{1}{N} \sum_{n=0}^{N-1}\left\vert x_n\right\vert^2$$   $$\mbox{(average power of $x$)}$$

Another common description when $x$ is real is the mean square. When $x$ is a complex sinusoid, i.e., $x(n) = Ae^{j(\omega nT + \phi)}$, then ${\cal P}_x = A^2$; in other words, for complex sinusoids, the average power equals the instantaneous power which is the amplitude squared. For real sinusoids, $y_n =$   re$\left\{x_n\right\}=A\cos(\omega nT+\phi)$, we have ${\cal P}_y = A^2/2$.

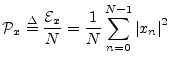
Power is always in physical units of energy per unit time. It therefore makes sense to define the average signal power as the total signal energy divided by its length. We normally work with signals which are functions of time. However, if the signal happens instead to be a function of distance (e.g., samples of displacement along a vibrating string), then the ``power'' as defined here still has the interpretation of a spatial energy density. Power, in contrast, is a temporal energy density.

The root mean square (RMS) level of a signal $x$ is simply $\sqrt{{\cal P}_x}$. However, note that in practice (especially in audio work) an RMS level is typically computed after subtracting out any nonzero mean value. Here, we call that the variance.

The variance (more precisely the sample variance) of the signal $x$ is defined as the power of the signal with its mean removed:^5.7

$$\sigma_x^2 \isdef \frac{1}{N}\sum_{n=0}^{N-1}\left\vert x_n - \mu_x\right\vert^2$$   $$\mbox{(sample variance of $x$)}$$

It is quick to show that, for real signals, we have

$$\sigma_x^2 = {\cal P}_x - \mu_x^2$$

which is the ``mean square minus the mean squared.'' We think of the variance as the power of the non-constant signal components (i.e., everything but dc). The terms ``sample mean'' and ``sample variance'' come from the field of statistics, particularly the theory of stochastic processes. The field of statistical signal processing [25,32,63] is firmly rooted in statistical topics such as ``probability,'' ``random variables,'' ``stochastic processes,'' and ``time series analysis.'' In this book, we will only touch lightly on a few elements of statistical signal processing in a self-contained way.

The norm (more specifically, the $L2$ norm, or Euclidean norm) of a signal $x$ is defined as the square root of its total energy:

$$\Vert x\Vert \isdef \sqrt{{\cal E}_x} = \sqrt{\sum_{n=0}^{N-1}\left\vert x_n\right\vert^2}$$   $$\mbox{(norm of $x$)}$$

We think of $\Vert x\Vert$ as the length of the vector $x$ in $N$-space. Furthermore, $\Vert x-y\Vert$ is regarded as the distance between $x$ and $y$. The norm can also be thought of as the ``absolute value'' or ``radius'' of a vector.^5.8