Definition. The frequency response of an LTI filter is defined
as the spectrum of the output signal divided by the spectrum of the
input signal.
In this section, we show that the frequency response is given by the
transfer function evaluated on the unit circle, i.e.,
![]() . We
then show that this is the same result we got using sine-wave analysis
in Chapter 1.
. We
then show that this is the same result we got using sine-wave analysis
in Chapter 1.
Beginning with Eq. (6.4), we have
A basic property of the z transform is that, over the unit circle
![]() ,
we find the spectrum [83]. To show this, we set
,
we find the spectrum [83]. To show this, we set
![]() in the definition of the z transform, Eq. (6.1), to obtain
in the definition of the z transform, Eq. (6.1), to obtain
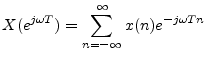
Applying this relation to
![]() gives
gives
This immediately implies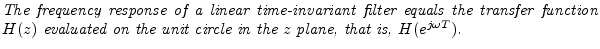
or
By Eq. (7.1), the frequency response specifies the gain and
phase shift applied by the filter at each frequency.
Since ![]() ,
, ![]() , and
, and ![]() are constants, the frequency response
are constants, the frequency response
![]() is only a function of radian frequency
is only a function of radian frequency ![]() . Since
. Since
![]() is real, the frequency response may be considered a
complex-valued function of a real variable. The response at frequency
is real, the frequency response may be considered a
complex-valued function of a real variable. The response at frequency
![]() Hz, for example, is
Hz, for example, is
![]() , where
, where ![]() is the sampling
period in seconds. It might be more convenient to define new
functions such as
is the sampling
period in seconds. It might be more convenient to define new
functions such as
![]() and write simply
and write simply
![]() instead of
having to write
instead of
having to write
![]() so often, but doing so would add a lot of new
functions to an already notation-rich scenario. Furthermore, writing
so often, but doing so would add a lot of new
functions to an already notation-rich scenario. Furthermore, writing
![]() makes explicit the connection between the transfer function
and the frequency response.
makes explicit the connection between the transfer function
and the frequency response.
Notice that defining the frequency response as a function of
![]() places the frequency ``axis'' on the unit circle in the complex
places the frequency ``axis'' on the unit circle in the complex
![]() plane, since
plane, since
![]() . As a result, adding multiples of the
sampling frequency to
. As a result, adding multiples of the
sampling frequency to ![]() corresponds to traversing
whole cycles around the unit circle, since
corresponds to traversing
whole cycles around the unit circle, since
We have seen that the spectrum is a particular slice through the
transfer function. It is also possible to go the other way and
generalize the spectrum (defined only over the unit circle) to the
entire ![]() plane by means of a mathematical process called
analytic continuation (see §B.2). Since analytic
continuation is unique (for all filters encountered in practice), we
get the same results going either direction.
plane by means of a mathematical process called
analytic continuation (see §B.2). Since analytic
continuation is unique (for all filters encountered in practice), we
get the same results going either direction.
Because every complex number can be represented as a magnitude and angle, the frequency response may be decomposed into two real-valued functions, the amplitude response and the phase response. Formally, we may define them as follows: