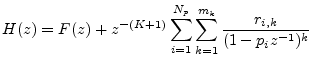
Instead of breaking up a filter into a series of second-order sections, as discussed in the previous section, we can break the filter up into a parallel sum of second-order sections. Parallel sections are based directly on the partial fraction expansion (PFE) of the filter transfer function discussed in §6.8. As discussed in §6.8.3, there is additionally an FIR part when the order of the transfer-function denominator does not exceed that of the numerator (i.e., when the transfer function is not strictly proper). The most general case of a PFE, valid for any finite-order transfer function, was given by Eq. (6.19), repeated here for convenience:
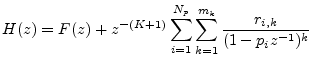
The FIR part is typically realized as a tapped delay line, as shown in Fig.5.5. For distinct poles, the recursive terms may be realized as a parallel sum of complex one-pole filter sections.