By superposition, we may readily generalize complex sinewave analysis
to the case in which ![]() is an arbitrary
superposition of input sinusoids:
is an arbitrary
superposition of input sinusoids:
![$\displaystyle x(n) \isdef \int_{-\pi/T}^{\pi/T}A(\omega) e^{j[\omega n T + \phi(\omega)]} d\omega
$](img963.png)
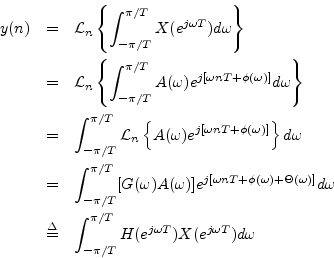
where ![]() is the amplitude response, and
is the amplitude response, and
![]() the
phase response of the LTI filter. We have thus shown by superposition
that, given any input signal
the
phase response of the LTI filter. We have thus shown by superposition
that, given any input signal ![]() , the output spectrum
, the output spectrum
![]() is
equal to the input spectrum
is
equal to the input spectrum
![]() multiplied by the frequency
response
multiplied by the frequency
response
![]() , where the frequency response can be measured one
frequency at a time using a sinusoidal input signal.
, where the frequency response can be measured one
frequency at a time using a sinusoidal input signal.
In contrast to the polar representation of frequency response
![]() , the real and imaginary parts
do not have such intuitively appealing individual
interpretations. Consequently, the polar form is usually preferred for
expressing filter responses as a function of frequency.
, the real and imaginary parts
do not have such intuitively appealing individual
interpretations. Consequently, the polar form is usually preferred for
expressing filter responses as a function of frequency.