Implementation

Given an activity-node graph, the objective of critical path analysis is to determine the slack time for each activity and thereby to identify the critical activities and the critical path. We shall assume that the activity node graph has already been transformed to an edge-node graph. The implementation of this transformation is left as a project for the reader (Project ). Therefore, the first step is to compute the earliest and latest event times.

According to Equation , the earliest event time of vertex w is obtained from the earliest event times of all its predecessors. Therefore, must compute the earliest event times in topological order. To do this, we define the EarliestTimeVisitor shown in Program .

  
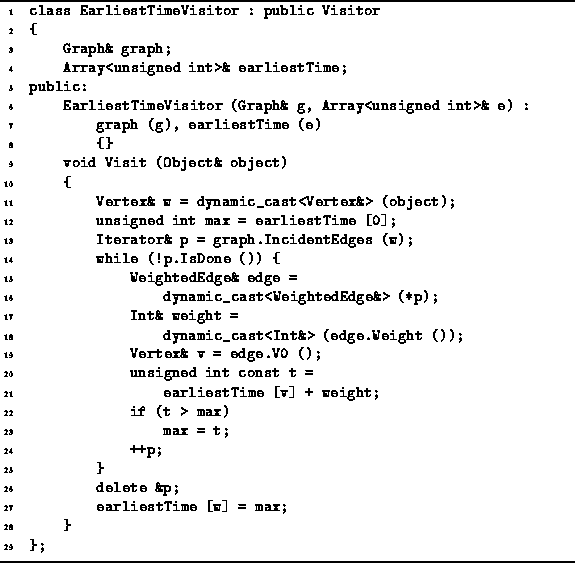
Program: Critical Path Analysis--Computing Earliest Event Times

The EarliestTimeVisitor has three member variables--graph, earliestTime and startTime. The first is a reference to the event-node graph; the second refers to an array used to record the values; and the third is the time at which the initial activity starts.

The Visit member function of the EarliestTimeVisitor class implements directly Equation . It uses an IncidentEdges iterator to determine all the predecessors of a given node and computes .

In order to compute the latest event times, it is necessary to define also a LatestTimeVisitor. This visitor must visit the vertices of the event-node graph in reverse topological order. Its implementation follows directly from Equation  and Program .

Program  defines the routine called CriticalPathAnalysis that does what its name implies. This routine takes as its lone argument a reference to a Digraph instance that represents an event-node graph. This implementation assumes that the edge weights are instances of the Int class defined in Program .

  
Program: Critical Path Analysis--Finding the Critical Paths

The routine first uses the EarliestTimeVisitor in a topological order traversal to compute the earliest event times which are recored in the earliestTime array (lines 5-8). Next, the latest event times are computed and recorded in the latestTime array. Notice that this is done using a LatestTimeVisitor in a postorder depth-first traversal (lines 10-13). This is because a postorder depth-first traversal is equivalent to a topological order traversal in reverse!

Once the earliest and latest event times have been found, we can compute the slack time for each edge. In the implementation shown, an edge-weighted graph is constructed that is isomorphic with the the original event-node graph, but in which the edge weights are the slack times as given by Equation  (lines 15-31). By constructing such a graph we can make use of Dijkstra's algorithm find the shortest path from start to finish since the shortest path must be the critical path (line 34).

The DijkstrasAlgorithm routine given in Section  returns its result in the form of a shortest-path graph. The shortest-path graph for the activity-node graph of Figure  is shown in Figure . By following the path in this graph from vertex 9 back to vertex 0, we find that the critical path is .

  
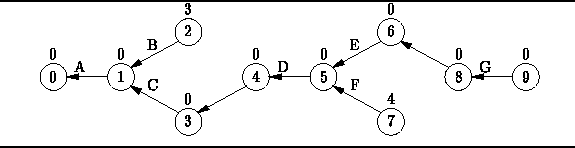
Figure: The Critical Path Graph corresponding to Figure 

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.