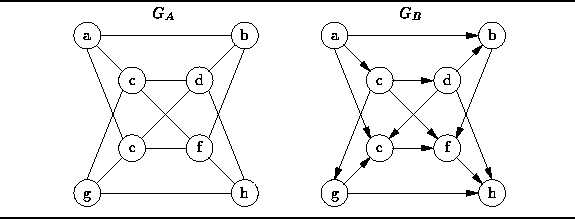
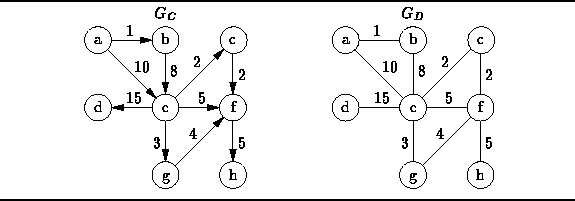
- Compute the in-degree of v.
- Compute the out-degree of v.
-
List the elements of
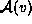 .
. -
List the elements of
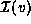 .
.
- Show how the graph is represented using an adjacency matrix.
- Show how the graph is represented using adjacency lists.
- List the order in which the nodes are visited in a preorder traversal.
- List the order in which the nodes are visited in a postorder traversal.
- How can we tell whether a given DAG is a tree?
- Devise an algorithm to test whether a given DAG is a tree.
- Devise an algorithm to count the number of connected components in a graph.
- Devise an algorithm that labels the vertices of a graph in such a way that all the vertices in a given connected component get the same label and vertices in different connected components get different labels.
![]()
How can we determine whether ![]() is a total order?
is a total order?