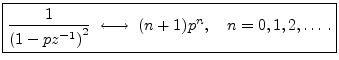
In the time domain, repeated poles give rise to polynomial amplitude envelopes on the decaying exponentials corresponding to the (stable) poles. For example, in the case of a single pole repeated twice, we have
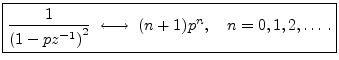
Proof:
First note that
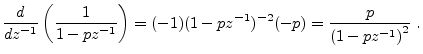
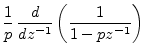 |
|||
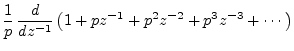 |
|||
 |
|||
| (7.13) |