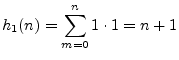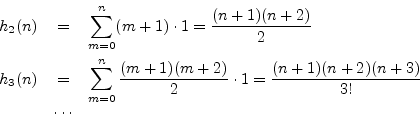So What's Up with Repeated Poles?

In the previous section, we found that repeated poles give rise to polynomial amplitude-envelopes multiplying the exponential decay due to the pole. On the other hand, two different poles can only yield a convolution (or sum) of two different exponential decays, with no polynomial envelope allowed. This is true no matter how closely the poles come together; the polynomial envelope can occur only when the poles merge exactly. This might violate one's intuitive expectation of a continuous change when passing from two closely spaced poles to a repeated pole.

To study this phenomenon further, consider the convolution of two one-pole impulse-responses $h_1(n) = p_1^n$ and $h_2(n) = p_2^n$:

$$h(n) \isdef (h_1\ast h_2)(n) = \sum_{m=0}^n h_1(m)h_2(n-m) = \sum... ...^n p_1^{m}p_2^{n-m} = p_2^n\sum_{m=0}^n \left(\frac{p_1}{p_2}\right)^m \protect$$ (7.14)

The finite limits on the summation result from the fact that both $h_1$ and $h_2$ are causal. Recall the closed-form sum of a truncated geometric series:

$$\sum_{m=0}^n r^m = \frac{1-r^{n+1}}{1-r}$$

Applying this to Eq. (6.14) yields

$$h(n) = p_2^n \frac{1-(p_1/p_2)^{n+1}}{1-(p_1/p_2)} = \frac{p_2^{n+1}-p_1^{n+1}}{p_2-p_1} = \frac{p_1^{n+1}-p_2^{n+1}}{p_1-p_2}.$$

Note that the result is symmetric in $p_1$ and $p_2$. If $\left\vert p_1\right\vert>\left\vert p_2\right\vert$, then $h(n)$ becomes proportional to $p_1^n$ for large $n$, while if $\left\vert p_2\right\vert>\left\vert p_1\right\vert$, it becomes instead proportional to $p_2^n$.

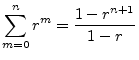
Going back to Eq. (6.14), we have

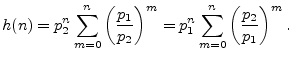$$h(n) = p_2^n\sum_{m=0}^n \left(\frac{p_1}{p_2}\right)^m = p_1^n\sum_{m=0}^n \left(\frac{p_2}{p_1}\right)^m.$$ (7.15)

Setting $p_1=p_2=p$ yields

$$h(n) = (n+1)p^n$$ (7.16)

which is the first-order polynomial amplitude-envelope case for a repeated pole. We can see that the transition from ``two convolved exponentials'' to ``single exponential with a polynomial amplitude envelope'' is perfectly continuous, as we would expect.

We also see that the polynomial amplitude-envelopes fundamentally arise from iterated convolutions. This corresponds to the repeated poles being arranged in series, rather than in parallel. The simplest case is when the repeated pole is at $p=1$, in which case its impulse response is a constant:

$$\frac{1}{1-z^{-1}} = 1 + z^{-1}+ z^{-2}+ \cdots \;\leftrightarrow\; [1,1,1,\ldots]$$

The convolution of a constant with itself is a ramp:

$$h_1(n)=\sum_{m=0}^n 1\cdot 1 = n+1$$

The convolution of a constant and a ramp is a quadratic, and so on:^7.6

$$\begin{eqnarray*} h_2(n)&=&\sum_{m=0}^n (m+1)\cdot 1 = \frac{(n+1)(n+2)}{2}\\ h... ...ac{(m+1)(m+2)}{2}\cdot 1=\frac{(n+1)(n+2)(n+3)}{3!}\\ &\cdots& \end{eqnarray*}$$