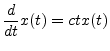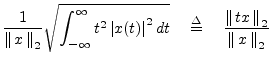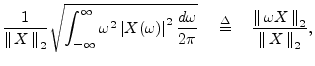Duration and Bandwidth as Second Moments

More interesting definitions of duration and bandwidth are obtained for nonzero signals using the normalized second moments of the squared magnitude:

$$\Delta t \isdef \frac{1}{\left\Vert\,x\,\right\Vert _2} \sqrt{\int_{-\infty}^\inf... ...sdef \quad \frac{\left\Vert\,tx\,\right\Vert _2}{\left\Vert\,x\,\right\Vert _2}$$

$$\Delta \omega \isdef \frac{1}{\left\Vert\,X\,\right\Vert _2} \sqrt{\int_{-\infty}^\inf... ...{\left\Vert\,\omega X\,\right\Vert _2}{\left\Vert\,X\,\right\Vert _2}, \protect$$ (C.1)

    where

$$\begin{eqnarray*} \nonumber \\ [10pt] \left\Vert\,x\,\right\Vert _2^2 &\isdef &... ...}^\infty \left\vert X(\omega)\right\vert^2 \frac{d\omega}{2\pi}. \end{eqnarray*}$$

By the DTFT power theorem, which is proved in a manner analogous to the DFT case in §7.4.8, we have $\left\Vert\,x\,\right\Vert _2=\left\Vert\,X\,\right\Vert _2$. Note that writing `` $\left\Vert\,tx\,\right\Vert _2$'' and `` $\left\Vert\,\omega X\,\right\Vert _2$'' is an abuse of notation, but a convenient one. These duration/bandwidth definitions are routinely used in physics, e.g., in connection with the Heisenberg uncertainty principle.^C.1Under these definitions, we have the following theorem [51, p. 273-274]:

Theorem: If $x(t) \ne 0$ and $\sqrt{\vert t\vert}\,x(t) \to 0$ as $\left\vert t\right\vert\to\infty$, then

$$\zbox {\Delta t\cdot \Delta \omega \geq \frac{1}{2}} \protect$$ (C.2)

with equality if and only if

$$x(t) = Ae^{-\alpha t^2}, \quad \alpha>0, \quad A\ne 0.$$

That is, only the Gaussian function (also known as the ``bell curve'' or ``normal curve'') achieves the lower bound on the time-bandwidth product.

Proof: Without loss of generality, we may take consider $x(t)$ to be real and normalized to have unit $L2$ norm ( $\left\Vert\,x\,\right\Vert _2=1$). From the Schwarz inequality (see §5.9.3 for the discrete-time case),

$$\left\vert\int_{-\infty}^\infty t x(t) \left[\frac{d}{dt}x(t)\rig... ...) dt \int_{-\infty}^\infty \left\vert\frac{d}{dt}x(t)\right\vert^2 dt. \protect$$ (C.3)

The left-hand side can be evaluated using integration by parts:

$$\int_{-\infty}^\infty tx \frac{dx}{dt} dt = \left . t \frac{x^2(t... ...ty x^2(t) dt \isdef -\frac{1}{2}\left\Vert\,x\,\right\Vert _2^2 = -\frac{1}{2}$$

where we used the assumption that $\sqrt{\vert t\vert}\,x(t) \to 0$ as $\left\vert t\right\vert\to\infty$.

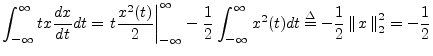
The second term on the right-hand side of Eq. (C.3) can be evaluated using the power theorem (§7.4.8 proves the discrete-time case) and differentiation theorem (§C.1 above):

$$\int_{-\infty}^\infty \left\vert\frac{dx(t)}{dt}\right\vert^2 dt ... ...\infty}^\infty \omega^2 \left\vert X(\omega)\right\vert^2 \frac{d\omega}{2\pi}$$

Substituting these evaluations into Eq. (C.3) gives

$$\left\vert-\frac{1}{2}\right\vert^2 \leq \left\Vert\,tx\,\right\Vert _2^2 \left\Vert\,\omega X\,\right\Vert _2^2.$$

Taking the square root of both sides gives the uncertainty relation sought.

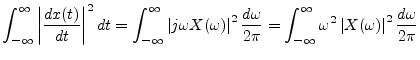
If equality holds in the uncertainty relation Eq. (C.2), then Eq. (C.3) implies

$$\frac{d}{dt}x(t) = c t x(t)$$

for some constant $c$, which implies $x(t)=A e^{\frac{c}{2} t^2}$ for some constants $A$ and $c$. Since $x(\pm\infty)=0$ by hypothesis, we have $c<0$ while $A\ne 0$ remains arbitrary.