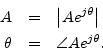
To illustrate the use of complex numbers in matlab, we repeat the previous sine-wave analysis of the simplest lowpass filter using complex sinusoids instead of real sinusoids.
Only the sine-wave analysis function needs to be rewritten, and it appears in Fig.2.10. The initial change is to replace the line
s = ampin * cos(2*pi*f(k)*t + phasein); % real sinusoidwith the line
s = ampin * e .^ (j*2*pi*f(k)*t + phasein); % complexAnother change in Fig.2.10 is that the plotsignals option is omitted, since a complex signal plot requires two real plots. This option is straightforward to restore if desired.
In the complex-sinusoid case, we find that measuring the amplitude and phase of the output signal is greatly facilitated. While we could use the previous method on either the real part or imaginary part of the complex output sinusoid, it is much better to measure its instananeous amplitude and instananeous phase by means of the formulas
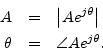
Furthermore, since we should obtain the same answer for each sample, we can average the results to minimize noise due to round-off error:
ampout = mean(abs(yss)); % avg instantaneous amplitude gains(k) = ampout/ampin; % amplitude response sample sss = s(ntransient+1:length(y)); % chop input like output phases(k) = mean(mod2pi(angle(yss.*conj(sss))));The expression angle(yss.*conj(sss)) in the last line above produces a vector of estimated filter phases which are the same for each sample (to within accumulated round-off errors), because the term
The final measured frequency response is plotted in Fig.2.9.
The test conditions were as in Fig.2.7, i.e., the highest
test frequency was fmax = ![]() , and the number of samples
in each test sinusoid was tmax
, and the number of samples
in each test sinusoid was tmax ![]() . Unlike the real
sine-wave analysis results in Fig.2.7, there is no visible
error associated with complex sine-wave analysis. Because
instantaneous amplitude and phase are available from every sample of a
complex sinusoid, there is no need for signal interpolation of any
kind. The only source of error is now round-off error, and even that
can be ``averaged out'' to any desired degree by enlarging the number
of samples in the complex sinusoids used to probe the system.
. Unlike the real
sine-wave analysis results in Fig.2.7, there is no visible
error associated with complex sine-wave analysis. Because
instantaneous amplitude and phase are available from every sample of a
complex sinusoid, there is no need for signal interpolation of any
kind. The only source of error is now round-off error, and even that
can be ``averaged out'' to any desired degree by enlarging the number
of samples in the complex sinusoids used to probe the system.
![\includegraphics[width=\twidth ]{eps/swanalcmain}](img268.png) |
This example illustrates some of the advantages of complex sinusoids over real sinusoids. Note also the ease with which complex vector quantities are manipulated in the matlab language.
function [gains,phases] = swanalc(t,f,B,A) % SWANALC - Perform COMPLEX sine-wave analysis on the % digital filter having transfer function % H(z) = B(z)/A(z) ampin = 1; % input signal amplitude phasein = 0; % input signal phase N = length(f); % number of test frequencies gains = zeros(1,N); % pre-allocate amp-response array phases = zeros(1,N); % pre-allocate phase-response array if length(A)==1, ntransient=length(B)-1, else error('Need to set transient response duration here'); end for k=1:length(f) % loop over analysis frequencies s = ampin*e.^(j*2*pi*f(k)*t+phasein); % test sinusoid y = filter(B,A,s); % run it through the filter yss = y(ntransient+1:length(y)); % chop off transient ampout = mean(abs(yss)); % avg instantaneous amplitude gains(k) = ampout/ampin; % amplitude response sample sss = s(ntransient+1:length(y)); % align with yss phases(k) = mean(mod2pi(angle(yss.*conj(sss)))); end |