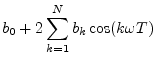A practical zero phase filter was illustrated in Figures 11.1 and 11.2. In this section, we look further at some simpler cases.
The trivial (non-) filter
![]() has frequency response
has frequency response
![]() , which is truly zero phase,
, which is truly zero phase,
Every second-order zero-phase FIR filter has an impulse response of the form
Extending the previous example, every order ![]() zero-phase FIR
filter has an impulse response of the form
zero-phase FIR
filter has an impulse response of the form