Given the transfer function ![]() , the frequency response is
obtained by evaluating it on the unit circle in the complex plane,
i.e., by setting
, the frequency response is
obtained by evaluating it on the unit circle in the complex plane,
i.e., by setting
![]() , where
, where ![]() is the sampling interval in
seconds, and
is the sampling interval in
seconds, and ![]() is radian frequency:4.3
is radian frequency:4.3
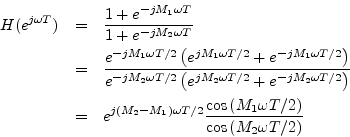
When
![]() , the frequency response is a ratio of cosines in
, the frequency response is a ratio of cosines in
![]() times a linear phase term
times a linear phase term
![]() (which
corresponds to a pure delay of
(which
corresponds to a pure delay of ![]() samples). This special case
gives insight into the behavior of the filter as its coefficients
samples). This special case
gives insight into the behavior of the filter as its coefficients
![]() and
and ![]() approach 1.
approach 1.
When
![]() , the filter degenerates to
, the filter degenerates to ![]() which
corresponds to
which
corresponds to ![]() ; in this case, the delayed input and output
signals cancel each other out. As a check, let's verify this in the
time domain:
; in this case, the delayed input and output
signals cancel each other out. As a check, let's verify this in the
time domain:
![\begin{eqnarray*}
y(n) &=& x(n) + x(n-M) - y(n-M)\\
&=& x(n) + x(n-M) - [x(n-M...
...) - y(n-3M)]\\
&=& x(n) + y(n-3M)\\
&=& \cdots\\
&=& x(n).
\end{eqnarray*}](img320.png)