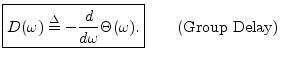
A more commonly encountered representation of filter phase response is called the group delay, defined by
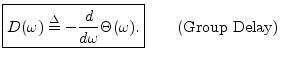
An example of a linear phase response is that of the simplest lowpass
filter,
![]() . Thus, both the phase delay and the group
delay of the simplest lowpass filter are equal to half a sample at
every frequency.
. Thus, both the phase delay and the group
delay of the simplest lowpass filter are equal to half a sample at
every frequency.
For any phase function, the group delay ![]() may be interpreted
as the time delay of the amplitude envelope of a sinusoid at
frequency
may be interpreted
as the time delay of the amplitude envelope of a sinusoid at
frequency ![]() [62]. The bandwidth of the amplitude
envelope in this interpretation must be restricted to a frequency
interval over which the phase response is approximately linear.
We derive this result in the next subsection.
[62]. The bandwidth of the amplitude
envelope in this interpretation must be restricted to a frequency
interval over which the phase response is approximately linear.
We derive this result in the next subsection.
Thus, the name ``group delay'' for ![]() refers to the fact that
it specifies the delay experienced by a narrow-band ``group'' of
sinusoidal components which have frequencies within a narrow frequency
interval about
refers to the fact that
it specifies the delay experienced by a narrow-band ``group'' of
sinusoidal components which have frequencies within a narrow frequency
interval about ![]() . The width of this interval is limited to
that over which
. The width of this interval is limited to
that over which ![]() is approximately constant.
is approximately constant.