Is Linear Phase Really Ideal in Audio Applications?

It is generally accepted that zero or linear phase filters are ideal for audio applications. This is because such filters delay all frequencies by the same amount, thereby maximally preserving waveshape. Mathematically, all Fourier-components passed by the filter remain time-synchronized exactly as they were in the original signal. However, this section will argue that a phase response somewhere between linear- and minimum-phase may be even better in some cases. We show this by means of a Matlab experiment comparing minimum-phase and zero-phase impulse responses.

The matlab code is shown in Fig.12.1. An order 8 elliptic-function lowpass filter [63] is designed with a cut-off frequency at 2 kHz. We choose an elliptic-function filter because it has a highly nonlinear phase response near its cut-off frequency, resulting in extra delay there which can be perceived as ``ringing'' at that frequency. The cut-off is chosen at 2kHz because this is a highly audible frequency. We want to clearly hear the ringing in this experiment in order to compare the zero-phase and minimum-phase cases.

Figure 12.1: Matlab script for listening to minimum-phase and zero-phase impulse responses having the same amplitude response.

 

% ellipt.m - Compare minimum-phase and zero-phase
%            lowpass impulse responses.

dosounds = 1;
N = 8;     % filter order
Rp = 0.5;  % passband ripple (dB)
Rs = 60;   % stopband ripple (-dB)
Fs = 8192; % default sampling rate (Windows Matlab)
Fp = 2000; % passband end
Fc = 2200; % stopband begins [gives order 8]
Ns = 4096; % number of samples in impulse responses

[B,A] = nellip(Rp, Rs, Fp/(0.5*Fs), Fc/(0.5*Fs)); % Octave
% [B,A] = ellip(N, Rp, Rs, Fp/(0.5*Fs)); % Matlab

% Minimum phase case:
imp = [1,zeros(1,Ns/2-1)]; % or 'h1=impz(B,A,Ns/2-1)'
h1 = filter(B,A,imp); % min-phase impulse response
hmp = filter(B,A,[h1,zeros(1,Ns/2)]); % apply twice

% Zero phase case:
h1r = fliplr(h1); % maximum-phase impulse response
hzp = filter(B,A,[h1r,zeros(1,Ns/2)]); % min*max=zp
% hzp = fliplr(hzp); % not needed here since symmetric

elliptplots; % plot impulse- and amplitude-responses

% Let's hear them!
while(dosounds)
  sound(hmp,Fs);
  pause(0.5);
  sound(hzp,Fs);
  pause(1);
end

Let the impulse response of the 8th order lowpass filter be denoted $h(n)$. It is minimum phase since there are no zeros outside the unit circle. (An elliptic-function filter actually has all of its zeros on the unit circle, and this is technically not allowed for minimum-phase filters. However, nothing changes if we move the zeros from radius 1 to radius $1-10^{-12}$, say, which would be allowed.)

From $h(n)$ we prepare two impulse responses having the same magnitude spectra but different phase spectra:

$$h_{\hbox{\tiny mp}}\isdef h\ast h,$$

which is minimum phase,^13.2 and

$$h_{\hbox{\tiny zp}}\isdef h\ast$$   FLIP$$(h),$$

which is zero phase, as discussed in §11.7. In both cases, the magnitude spectrum is

$$\left\vert H_{\hbox{mp}}(e^{j\omega T})\right\vert = \left\vert H... ...box{zp}}(e^{j\omega T})\right\vert = \left\vert H(e^{j\omega T})\right\vert^2,$$

while the phase spectra are

$$\begin{eqnarray*} \angle{H_{\hbox{mp}}(e^{j\omega T})} &=& 2\angle{H(e^{j\omega T})}\\ \angle{H_{\hbox{zp}}(e^{j\omega T})} &=& 0, \end{eqnarray*}$$

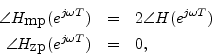
again as discussed in §11.7.

Since we are listening to a lowpass filtered impulse, it is reasonable to define the ideal expected sound as a ``lowpass-filtered click.'' We may therefore ask which signal sounds more like a lowpassed click, $h_{\hbox{\tiny mp}}$ or $h_{\hbox{\tiny zp}}$? In the minimum-phase case, all filter ringing occurs after the main pulse, while in the zero-phase case, it is equally divided before and after the main pulse (see Fig.12.2). Listening tests confirm that the ``pre-ring'' of the zero-phase case is audible before the main click, giving it a kind of ``chirp'' quality. You can draw your own conclusions, but I would say the minimum-phase case is a better ``click''. Since forward masking is stronger than backward masking in hearing perception, the optimal distribution of ringing is probably a small amount before and the rest after the main pulse.

Figure 12.2: Minimum-phase and zero-phase impulse responses derived from two applications of an order 8 elliptic-function lowpass filter.

Figure 12.3 verifies that the magnitude spectra are the same in each case.

Figure 12.3: Magnitude spectra of minimum-phase and zero-phase impulse responses derived from two passes through an order 8 elliptic-function lowpass filter.