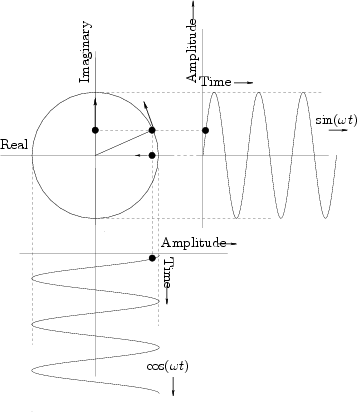
Figure 1.8 shows Euler's relation graphically as it applies to
sinusoids. A point traveling with uniform velocity around a circle
with radius 1 may be represented by
![]() in
the complex plane, where
in
the complex plane, where ![]() is time and
is time and ![]() is the number of
revolutions per second. The projection of this motion onto the
horizontal (real) axis is
is the number of
revolutions per second. The projection of this motion onto the
horizontal (real) axis is
![]() , and the projection onto
the vertical (imaginary) axis is
, and the projection onto
the vertical (imaginary) axis is
![]() . For
discrete-time circular motion, replace
. For
discrete-time circular motion, replace ![]() by
by ![]() to get
to get
![]() which may be interpreted as a
point which jumps an arc length
which may be interpreted as a
point which jumps an arc length
![]() radians along the circle
each sampling instant.
radians along the circle
each sampling instant.
 |
For circular motion to ensue, the sinusoidal motions must be at the same frequency, one-quarter cycle out of phase, and perpendicular (orthogonal) to each other. (With phase differences other than one-quarter cycle, the motion is generally elliptical.)
The converse of this is also illuminating. Take the usual circular
motion
![]() which spins counterclockwise along the unit
circle as
which spins counterclockwise along the unit
circle as ![]() increases, and add to it a similar but clockwise
circular motion
increases, and add to it a similar but clockwise
circular motion
![]() . This is shown in
Fig.1.9. Next apply Euler's identity to get
. This is shown in
Fig.1.9. Next apply Euler's identity to get
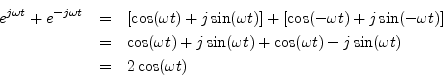
Thus,
This statement is a graphical or geometric interpretation of Eq. (1.11). A similar derivation (subtracting instead of adding) gives the sine identity Eq. (1.12).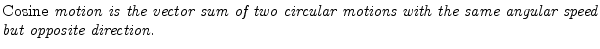
We call
![]() a positive-frequency sinusoidal
component when
a positive-frequency sinusoidal
component when
![]() , and
, and
![]() is the
corresponding negative-frequency component. Note that both
sine and cosine signals have equal-amplitude positive- and
negative-frequency components (see also [83,53]). This
happens to be true of every real signal (i.e., non-complex). To
see this, recall that every signal can be represented as a sum of
complex sinusoids at various frequencies (its Fourier
expansion). For the signal to be real, every positive-frequency
complex sinusoid must be summed with a negative-frequency sinusoid of
equal amplitude. In other words, any counterclockwise circular motion
must be matched by an equal and opposite clockwise circular motion in
order that the imaginary parts always cancel to yield a real signal
(see Fig.1.9). Thus, a real signal always has a magnitude
spectrum which is symmetric about 0 Hz. Fourier symmetries such as
this are developed more completely in [83].
is the
corresponding negative-frequency component. Note that both
sine and cosine signals have equal-amplitude positive- and
negative-frequency components (see also [83,53]). This
happens to be true of every real signal (i.e., non-complex). To
see this, recall that every signal can be represented as a sum of
complex sinusoids at various frequencies (its Fourier
expansion). For the signal to be real, every positive-frequency
complex sinusoid must be summed with a negative-frequency sinusoid of
equal amplitude. In other words, any counterclockwise circular motion
must be matched by an equal and opposite clockwise circular motion in
order that the imaginary parts always cancel to yield a real signal
(see Fig.1.9). Thus, a real signal always has a magnitude
spectrum which is symmetric about 0 Hz. Fourier symmetries such as
this are developed more completely in [83].