The Simplest Lowpass Filter

Let's start with a very basic example of the generic problem at hand: understanding the effect of a digital filter on the spectrum of a digital signal. The purpose of this example is to provide motivation for the general theory discussed in later chapters.

Figure 1.1: Amplitude response (gain versus frequency) specification for the ideal low-pass filter.

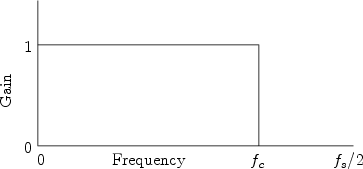
Our example is the simplest possible low-pass filter. A low-pass filter is one which does not affect low frequencies and rejects high frequencies. The function giving the gain of a filter at every frequency is called the amplitude response (or magnitude frequency response). The amplitude response of the ideal lowpass filter is shown in Fig.1.1. It is unity (1) for frequencies between 0 Hz and the cutoff frequency $f_c$ Hz, and it is 0 for all higher frequencies. The output spectrum is obtained by multiplying the input spectrum by the function shown.