A problem with equation-error methods is that stability of the filter
design is not guaranteed. When an unstable design is encountered,
one common remedy is to reflect unstable poles inside the unit circle,
leaving the magnitude response unchanged while modifying the phase of the
approximation in an ad hoc manner. This requires polynomial factorization
of
![]() to find the filter poles, which is typically more work
than the filter design itself.
to find the filter poles, which is typically more work
than the filter design itself.
A better way to address the instability problem is to repeat the
filter design employing a bulk delay. This amounts to
replacing
![]() by
by
Unstable equation-error designs are especially likely when
![]() is
noncausal. Since there are no constraints on where the poles of
is
noncausal. Since there are no constraints on where the poles of
![]() can be, one can expect unstable designs for desired
frequency-response functions having a linear phase trend with positive
slope.
can be, one can expect unstable designs for desired
frequency-response functions having a linear phase trend with positive
slope.
In the other direction, experience has shown that best results are obtained
when ![]() is minimum phase, i.e., when all the zeros of
is minimum phase, i.e., when all the zeros of ![]() are
inside the unit circle. For a given magnitude,
are
inside the unit circle. For a given magnitude,
![]() ,
minimum phase gives the maximum concentration of impulse-response energy
near the time origin
,
minimum phase gives the maximum concentration of impulse-response energy
near the time origin ![]() . Consequently, the impulse-response tends to start
large and decay immediately. For non-minimum phase
. Consequently, the impulse-response tends to start
large and decay immediately. For non-minimum phase ![]() , the
impulse-response
, the
impulse-response ![]() may be small for the first
may be small for the first ![]() samples, and the
equation error method can yield very poor filters in these cases. To see
why this is so, consider a desired impulse-response
samples, and the
equation error method can yield very poor filters in these cases. To see
why this is so, consider a desired impulse-response ![]() which is zero
for
which is zero
for
![]() , and arbitrary thereafter. Transforming
, and arbitrary thereafter. Transforming ![]() into the
time domain yields
into the
time domain yields
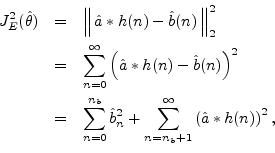
where ``![]() '' denotes convolution, and the additive decomposition
is due the fact that
'' denotes convolution, and the additive decomposition
is due the fact that
![]() for
for
![]() . In this case the
minimum occurs for
. In this case the
minimum occurs for
![]() ! Clearly this is
not a particularly good fit. Thus, the introduction of bulk-delay to guard
against unstable designs is limited by this phenomenon.
! Clearly this is
not a particularly good fit. Thus, the introduction of bulk-delay to guard
against unstable designs is limited by this phenomenon.
It should be emphasized that for minimum-phase
![]() ,
equation-error methods are very effective. It is simple to convert a
desired magnitude response into a minimum-phase frequency-response
by use of cepstral techniques [23,60] (see also the
appendix below), and this is highly recommended when minimizing equation
error. Finally, the error weighting by
,
equation-error methods are very effective. It is simple to convert a
desired magnitude response into a minimum-phase frequency-response
by use of cepstral techniques [23,60] (see also the
appendix below), and this is highly recommended when minimizing equation
error. Finally, the error weighting by
![]() can usually be
removed by a few iterations of the Steiglitz-McBride algorithm.
can usually be
removed by a few iterations of the Steiglitz-McBride algorithm.