As defined earlier in §5.6 (page ![]() ), a
filter is said to be stable if its impulse response
), a
filter is said to be stable if its impulse response ![]() decays to 0 as
decays to 0 as ![]() goes to infinity. Unstable filters are not normally
useful in practice because their output grows exponentially, even
while the input signal is zero, eventually overflowing the computer
word. The physical counterpart of an unstable filter is something
that will never stop quivering after you hit it with a hammer (or,
worse, will begin to shake more and more violently, like a washing
machine with boots in it).
goes to infinity. Unstable filters are not normally
useful in practice because their output grows exponentially, even
while the input signal is zero, eventually overflowing the computer
word. The physical counterpart of an unstable filter is something
that will never stop quivering after you hit it with a hammer (or,
worse, will begin to shake more and more violently, like a washing
machine with boots in it).
In terms of poles and zeros, an irreducible filter transfer function
is stable if and only if all the poles are inside the unit circle in
the ![]() plane (as first discussed in §6.8.6). This is because
the transfer function is the z transform of the impulse response, and if
there is an observable pole outside the unit circle, then there is an
exponentially increasing component of the impulse response. To see
this, consider a causal impulse response of the form
plane (as first discussed in §6.8.6). This is because
the transfer function is the z transform of the impulse response, and if
there is an observable pole outside the unit circle, then there is an
exponentially increasing component of the impulse response. To see
this, consider a causal impulse response of the form
The signal
![]() has the z transform
has the z transform
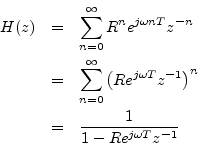
where the last step holds for
![]() , which is
true whenever
, which is
true whenever
![]() . Thus, the transfer function consists of a single pole at
. Thus, the transfer function consists of a single pole at
![]() , and it exists for
, and it exists for ![]() .9.1Now consider what happens when we let
.9.1Now consider what happens when we let ![]() become
greater than 1. The pole of
become
greater than 1. The pole of ![]() moves outside the unit circle, and
the impulse response has an exponentially increasing amplitude. (Note
moves outside the unit circle, and
the impulse response has an exponentially increasing amplitude. (Note
![]() .) Thus, the definition of stability is
violated. Since the z transform exists only for
.) Thus, the definition of stability is
violated. Since the z transform exists only for
![]() , we
see that
, we
see that ![]() implies that the z transform no longer exists on
the unit circle, so that the frequency response becomes undefined!
implies that the z transform no longer exists on
the unit circle, so that the frequency response becomes undefined!
The above one-pole analysis shows that a one-pole filter is stable if and only if its pole is inside the unit circle. In the case of an arbitrary transfer function, inspection of its partial fraction expansion (§6.8) shows that the behavior near any pole approaches that of a one-pole filter consisting of only that pole. Therefore, all poles must be inside the unit circle for stability.
In summary, a necessary and sufficient condition for the stability of any finite-order LTI filter is that all its poles lie strictly inside the unit circle. Poles on the unit circle may be called marginally stable. The impulse response component corresponding to a single pole on the unit circle never decays, but neither does it grow.9.2 In physical modeling applications, marginally stable poles occur often in lossless systems, such as ideal vibrating string models [86].