In the previous section, we found
![]() when
when ![]() is
real. This fact is of high practical importance. It says that the
spectrum of every real signal is Hermitian.
Due to this symmetry, we may discard all negative-frequency spectral
samples of a real signal and regenerate them later if needed from the
positive-frequency samples. Also, spectral plots of real signals are
normally displayed only for positive frequencies; e.g., spectra of
sampled signals are normally plotted over the range 0 Hz to
is
real. This fact is of high practical importance. It says that the
spectrum of every real signal is Hermitian.
Due to this symmetry, we may discard all negative-frequency spectral
samples of a real signal and regenerate them later if needed from the
positive-frequency samples. Also, spectral plots of real signals are
normally displayed only for positive frequencies; e.g., spectra of
sampled signals are normally plotted over the range 0 Hz to ![]() Hz. On the other hand, the spectrum of a complex signal must
be shown, in general, from
Hz. On the other hand, the spectrum of a complex signal must
be shown, in general, from ![]() to
to ![]() (or from 0 to
(or from 0 to ![]() ),
since the positive and negative frequency components of a complex
signal are independent.
),
since the positive and negative frequency components of a complex
signal are independent.
Recall from §7.3 that a signal ![]() is said to be
even if
is said to be
even if
![]() , and odd if
, and odd if
![]() . Below
are are Fourier theorems pertaining to even and odd signals and/or
spectra.
. Below
are are Fourier theorems pertaining to even and odd signals and/or
spectra.
Theorem: If
![]() , then
re
, then
re![]() is even and
im
is even and
im![]() is odd.
is odd.
Proof: This follows immediately from the conjugate symmetry of ![]() for real signals
for real signals
![]() .
.
Theorem: If
![]() ,
,
![]() is even and
is even and ![]() is odd.
is odd.
Proof: This follows immediately from the conjugate symmetry of ![]() expressed
in polar form
expressed
in polar form
![]() .
.
The conjugate symmetry of spectra of real signals is perhaps the most important symmetry theorem. However, there are a couple more we can readily show:
Theorem: An even signal has an even transform:
Proof:
Express ![]() in terms of its real and imaginary parts by
in terms of its real and imaginary parts by
![]() . Note that for a complex signal
. Note that for a complex signal ![]() to be even, both its real and
imaginary parts must be even. Then
to be even, both its real and
imaginary parts must be even. Then
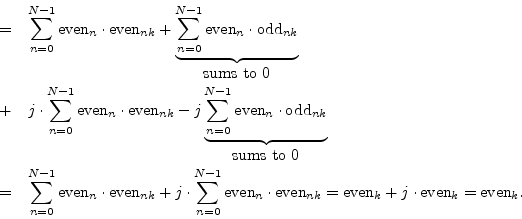
Theorem: A real even signal has a real even transform:
Proof: This follows immediately from setting ![]() in the preceding
proof. From Eq. (7.7), we are left with
in the preceding
proof. From Eq. (7.7), we are left with
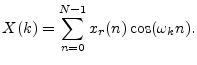
Instead of adapting the previous proof, we can show it directly:
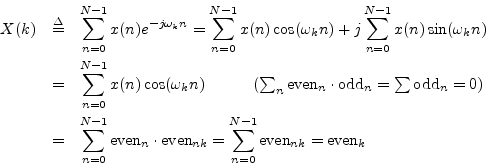
Definition: A signal with a real spectrum (such as any real, even signal)
is often called a zero phase signal. However, note that when
the spectrum goes negative (which it can), the phase is really
![]() , not 0. When a real spectrum is positive at dc (i.e.,
, not 0. When a real spectrum is positive at dc (i.e.,
![]() ), it is then truly zero-phase over at least some band
containing dc (up to the first zero-crossing in frequency). When the
phase switches between 0 and
), it is then truly zero-phase over at least some band
containing dc (up to the first zero-crossing in frequency). When the
phase switches between 0 and ![]() at the zero-crossings of the
(real) spectrum, the spectrum oscillates between being zero phase and
``constant phase''. We can say that all real spectra are
piecewise constant-phase spectra, where the two constant values
are 0 and
at the zero-crossings of the
(real) spectrum, the spectrum oscillates between being zero phase and
``constant phase''. We can say that all real spectra are
piecewise constant-phase spectra, where the two constant values
are 0 and ![]() (or
(or ![]() , which is the same phase as
, which is the same phase as ![]() ). In
practice, such zero-crossings typically occur at low magnitude, such
as in the ``side-lobes'' of the DTFT of an FFT window (see
Chapter 8).
). In
practice, such zero-crossings typically occur at low magnitude, such
as in the ``side-lobes'' of the DTFT of an FFT window (see
Chapter 8).