| (11.6) |
Normally when we need a resonator, we think immediately of the two-pole resonator. However, there is also a complex one-pole resonator having the transfer function
Since the impulse response is the inverse z transform of the transfer function, we can write down the impulse response of the complex one-pole resonator by recognizing Eq. (10.6) as the closed-form sum of an infinite geometric series, yielding
![$\displaystyle u(n) \isdef \left\{\begin{array}{ll}
1, & n\geq 0 \\ [5pt]
0, & n<0 \\
\end{array}\right.
$](img1278.png)
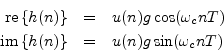
These may be called phase-quadrature sinusoids, since their phases differ by 90 degrees. The phase quadrature relationship for two sinusoids means that they can be regarded as the real and imaginary parts of a complex sinusoid.
By allowing ![]() to be complex,
to be complex,
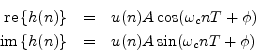
The frequency response of the complex one-pole resonator differs from
that of the two-pole real resonator in that the resonance
occurs only for one positive or negative frequency ![]() , but not
both. As a result, the resonance frequency
, but not
both. As a result, the resonance frequency ![]() is also the
frequency where the peak-gain occurs; this is only true in
general for the complex one-pole resonator. In particular, the peak
gain of a real two-pole filter does not occur exactly at resonance, except
when
is also the
frequency where the peak-gain occurs; this is only true in
general for the complex one-pole resonator. In particular, the peak
gain of a real two-pole filter does not occur exactly at resonance, except
when
![]() ,
, ![]() , or
, or ![]() . See
§10.6 for more on peak-gain versus resonance-gain (and how to
normalize them in practice).
. See
§10.6 for more on peak-gain versus resonance-gain (and how to
normalize them in practice).