Time-Varying Two-Pole Filters

It is quite common to want to vary the resonance frequency of a resonator in real time. This is a special case of a tunable filter. In the pre-digital days of analog synthesizers, filter modules were tuned by means of control voltages, and were thus called voltage-controlled filters (VCF). In the digital domain, control voltages are replaced by time-varying filter coefficients. In the time-varying case, the choice of filter structure has a profound effect on how the filter characteristics vary with respect to coefficient variations. In this section, we will take a look at the time-varying two-pole resonator.

Evaluating the transfer function of the two-pole resonator (Eq. (10.1)) at the point $e^{j\theta_c}$ on the unit circle (the filter's resonance frequency $\omega_c=\theta_c/T$) yields a gain at resonance equal to

$$H(e^{j\theta_c}) = \frac{b_0}{(1-Re^{j\theta_c}e^{-j\theta_c})(1-Re^{-j\theta_c}e^{-j\theta_c})}$$

$$= \frac{b_0}{1-R}\cdot \frac{1}{1-Re^{-j2\theta_c}} \protect$$ (11.11)

For simplicity, let $b_0 = 1$ in what follows. In the special cases $\theta_c=0$ (resonance at dc) and $\theta_c=\pi$ (resonance at $f=f_s/2$), we have

$$H(\pm1) = \frac{1}{(1-R)^2} \protect$$ (11.12)

Since $R$ is real, we have already found the gain (amplitude response) at a dc or $f_s/2$ resonance:

$$G(0) = G(\pi/T) \isdef \left\vert H(\pm1)\right\vert = \left\vert\frac{1}{(1-R)^2}\right\vert = \frac{1}{(1-R)^2}$$

In the middle frequency between dc and $f_s/2$, $\theta_c = \omega_c T = \pi/2$, Eq. (10.11) with $b_0 = 1$ becomes

$$H(j) = \frac{1}{(1-Re^{j2\frac{\pi}{2}})(1-R)} = \frac{1}{(1+R)(1-R)} = \frac{1}{1-R^2}$$

and, since $H(j)$ is real and positive, it coincides with the amplitude response, i.e., $H(j)=G(\pi/2)=1/(1-R^2)$.

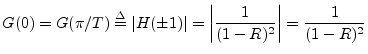
An important fact we can now see is that the gain at resonance depends markedly on the resonance frequency. In particular, the ratio of the two cases just analyzed is

$$\left\vert\frac{H(1)}{H(j)}\right\vert = \frac{1-R^2}{(1-R)^2} = ... ...R}{1-R} = \frac{\hbox{maximum resonance gain}}{\hbox{minimum resonance gain}}$$

We did not show that resonance gain is maximized at $e^{j\theta_c}=\pm 1$ and minimized at $e^{j\theta_c}=\pm j$, but this is straightforward to show, and strongly suggested by Fig.10.18 (and Fig.10.10).

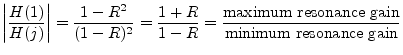
Note that the ratio of the dc resonance gain to the $f_s/4$ resonance gain is unbounded! The sharper the resonance (the closer $R$ is to 1), the greater the disparity in the gain.

Figure 10.18 illustrates a number of resonator frequency responses for the case $R=0.99$. (Resonators in practice may use values of $R$ even closer to 1 than this--even the case $R=1$ is used for making recursive digital sinusoidal oscillators [90].) For resonator tunings at dc and $f_s/2$, we predict the resonance gain to be $20\log_{10}[1/(1-R)^2] = -20\log_{10}[(1-0.99)^2] = -40\log_{10}(0.01) = 80$ dB, and this is what we see in the plot. When the resonance is tuned to $f_s/4$, the gain drops well below 40 dB. Clearly, we will need to compensate this gain variation when trying to use the two-pole digital resonator as a tunable filter.

Figure 10.18: Frequency response overlays for the two-pole resonator $H(z)=1/(1-2R\cos (\theta _c)z^{-1}+ R^2z^{-2})$, for $R=0.99$ and 10 values of $\theta _c$ uniformly spaced from 0 to $\pi$. The 5th case is plotted using thicker lines.

Figure 10.19 shows the same type of plot for the complex one-pole resonator $H(z)=1/(1-Re^{j\theta _c}z^{-1})$, for $R=0.99$ and 10 values of $\theta _c$. In this case, we expect the frequency response evaluated at the center frequency to be $H(e^{j\omega_c T}) =1/(1-Re^{j\theta_c}e^{-j\theta_c})=1/(1-R)$. Thus, the gain at resonance for the plotted example is $1/(1-0.99)=100=40$ db for all tunings. Furthermore, for the complex resonator, the resonance gain is also exactly equal to the peak gain.

Figure 10.19: Frequency response overlays for the one-pole complex resonator $H(z)=1/(1-Re^{j\theta _c}z^{-1})$, for $R=0.99$ and 10 values of $\theta _c$ uniformly spaced from 0 to $\pi$. The 5th case is plotted using thicker lines.