Definition: A linear, time-invariant filter
This appendix addresses the general problem of characterizing all digital allpass filters, including multi-input, multi-output (MIMO) allpass filters. As a result of including the MIMO case, the mathematical level is a little higher than usual for this book. The reader in need of more background is referred to [83,37,98].Our first task is to show that losslessness implies allpass.
Definition:
A linear, time-invariant filter ![]() is said to be
lossless if it preserves signal
energy for every input signal. That is, if the input signal is
is said to be
lossless if it preserves signal
energy for every input signal. That is, if the input signal is
![]() , and the output signal is
, and the output signal is
![]() , then we have
, then we have
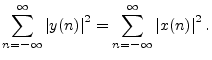
Notice that only stable filters can be lossless, since otherwise
![]() can be infinite while
can be infinite while
![]() is finite. We further
assume all filters are causalD.1 for
simplicity. It is straightforward to show the following:
is finite. We further
assume all filters are causalD.1 for
simplicity. It is straightforward to show the following:
Theorem: A stable, linear, time-invariant (LTI) filter transfer function
![]() is lossless if and only if
is lossless if and only if
Proof: We allow the signals ![]() and filter impulse response
and filter impulse response
![]() to be complex. By Parseval's theorem
[83] for the DTFT, we have,D.2 for any signal
to be complex. By Parseval's theorem
[83] for the DTFT, we have,D.2 for any signal
![]() ,
,
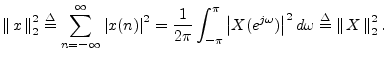
We have shown that every lossless filter is allpass. Conversely, every unity-gain allpass filter is lossless.