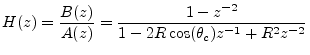 |
(11.14) |
It is surprisingly easy to normalize exactly the peak gain in a second-order resonator tuned by a single coefficient [94]. The filter structure that accomplishes this is the one we already considered in §10.6.1:
The peak gain is ![]() , so multiplying the transfer function by
, so multiplying the transfer function by
![]() normalizes the peak gain to one for all tunings. It can
also be shown [94] that the peak gain coincides with the
variance gain when the resonator is driven by white noise. That
is, if the variance of the driving noise is
normalizes the peak gain to one for all tunings. It can
also be shown [94] that the peak gain coincides with the
variance gain when the resonator is driven by white noise. That
is, if the variance of the driving noise is ![]() , the variance
of the noise at the resonator output is
, the variance
of the noise at the resonator output is
![]() .
Therefore, scaling the resonator input by
.
Therefore, scaling the resonator input by
![]() will
normalize the resonator such that the output signal power equals the
input signal power when the input signal is white noise.
will
normalize the resonator such that the output signal power equals the
input signal power when the input signal is white noise.
Frequency response overlays for the constant-peak-gain resonator are
shown in Fig.10.24 (![]() ), Fig.10.21
(
), Fig.10.21
(![]() ), and Fig.10.22 (
), and Fig.10.22 (![]() ). While the peak
frequency may be far from the resonance tuning in the more heavily
damped examples, the peak gain is always normalized to unity. The
normalized radian frequency
). While the peak
frequency may be far from the resonance tuning in the more heavily
damped examples, the peak gain is always normalized to unity. The
normalized radian frequency
![]() at which the peak gain
occurs is related to the pole angle
at which the peak gain
occurs is related to the pole angle
![]() by
[94]
by
[94]
Thus, ![]() must be close to 1 to obtain a resonant peak near dc (a case
commonly needed in audio work) or half the sampling rate (rarely
needed in practice). When
must be close to 1 to obtain a resonant peak near dc (a case
commonly needed in audio work) or half the sampling rate (rarely
needed in practice). When ![]() is much less than 1, the peak frequency
is much less than 1, the peak frequency
![]() cannot leave a small interval near one-fourth the sampling
rate, as can be seen at the far left in Fig.10.23.
cannot leave a small interval near one-fourth the sampling
rate, as can be seen at the far left in Fig.10.23.
Figure 10.23 predicts that for ![]() , the lowest peak-gain
frequency should be around
, the lowest peak-gain
frequency should be around
![]() radian per sample.
Figure 10.22 agrees with this prediction.
radian per sample.
Figure 10.22 agrees with this prediction.
As Figures 10.24 through 10.26 shows, the peak gain remains
constant even at very low and very high frequencies, to the extent
they are reachable for a given ![]() . The zeros at dc and
. The zeros at dc and ![]() preclude the possibility of peaks at exactly those frequencies, but
for
preclude the possibility of peaks at exactly those frequencies, but
for ![]() near 1, we can get very close to having a peak at dc or
near 1, we can get very close to having a peak at dc or
![]() , as shown in Figures 10.20 and 10.21.
, as shown in Figures 10.20 and 10.21.
![\includegraphics[width=\twidth ]{eps/cpgresgain}](img1421.png) |
![\includegraphics[width=\twidth ]{eps/cpgresgaindamped}](img1422.png) |
![\includegraphics[width=\twidth ]{eps/cpgresgaindampedp5}](img1423.png) |