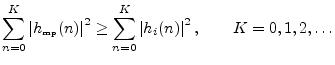Definition. An LTI filter
In Chapter 11 we looked at linear-phase and zero-phase digital filters. While such filters preserve waveshape, there are times when the linearity of the phase response is not important. In such cases, it is valuable to allow the phase to be arbitrary, or else to set it in such a way that the amplitude response is easier to match. In many cases, this means specifying minimum phase.
Definition. An LTI filteris said to be minimum phase if all its poles and zeros are inside the unit circle
(excluding the unit circle itself).
Note that minimum-phase filters are stable by definition since the
poles must be inside the unit circle. In addition, because the zeros
must also be inside the unit circle, the inverse filter ![]() is
also stable when
is
also stable when ![]() is minimum phase. One can say that
minimum-phase filters form an algebraic group in which the
group elements are impulse-responses and the group operation is
convolution (or, more specifically, the elements may be transfer
functions of a given order, and the group operation multiplication).
is minimum phase. One can say that
minimum-phase filters form an algebraic group in which the
group elements are impulse-responses and the group operation is
convolution (or, more specifically, the elements may be transfer
functions of a given order, and the group operation multiplication).
A minimum phase filter is also causal since noncausal terms in
the impulse response correspond to poles at infinity. The simplest
example of this would be the unit-sample advance, ![]() ,
which consists of a zero at
,
which consists of a zero at ![]() and a pole at
and a pole at ![]() .13.1
.13.1
A filter is minimum phase if both the numerator and denominator of its
transfer function are
minimum-phase polynomials
in ![]() :
:
Definition. A polynomial of the form
is said to be minimum phase if all of its rootsare inside the unit circle, i.e.,
.
We may also define a minimum-phase signal (or sequence) as the inverse z transform of a minimum-phase polynomial:
Definition. A signal,
, is said to be minimum phase if its z transform
is minimum phase.
Note that every stable, all-pole, (causal) filter
![]() is minimum phase, because stability implies that
is minimum phase, because stability implies that
![]() is minimum phase, and there are ``no zeros'' (all are at
is minimum phase, and there are ``no zeros'' (all are at
![]() ). This is an indication that minimum phase is in some sense the
most ``natural'' phase for a digital filter to have, since it is the
only phase available to a stable, causal, all-pole filter.
). This is an indication that minimum phase is in some sense the
most ``natural'' phase for a digital filter to have, since it is the
only phase available to a stable, causal, all-pole filter.
The effect of non-minimum-phase zeros on the complex cepstrum was described in §8.4.
The opposite of minimum phase is maximum phase:
If zeros of
Definition. An LTI filteris said to be maximum phase if all zeros of the polynomial
are outside the unit circle.
If ![]() is minimum phase, then
is minimum phase, then ![]() is maximum phase, and vice
versa.
is maximum phase, and vice
versa.
By the flip theorem for z transforms,
Example
An easy case to classify is the set of all first-order FIR filters
Among all signalshaving the identical magnitude spectra, the minimum-phase signal
has the fastest decay in the sense that