The complex cepstrum of a sequence ![]() is typically defined
as the inverse Fourier transform of its log spectrum
[60]
is typically defined
as the inverse Fourier transform of its log spectrum
[60]
![$\displaystyle {\tilde h}(n)\isdef \frac{1}{2\pi}\int_{-\pi}^\pi \ln[H(e^{j\omega})] e^{j\omega n}d\omega,
$](img1147.png)
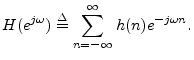
From Eq. (8.2), the log z transform can be written in terms of the
factored form as
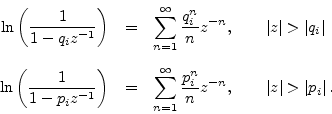
Since the region of convergence of the z transform must include the unit
circle (where the spectrum (DTFT) is defined), we see that the
Maclaurin expansion gives us the inverse z transform of all terms of
Eq. (8.9) corresponding to poles and zeros inside the unit
circle of the ![]() plane. Since the poles must be inside the unit
circle anyway for stability, this restriction is normally not binding
for the poles. However, zeros outside the unit circle--so-called
``non-minimum-phase zeros''--are used quite often in practice.
plane. Since the poles must be inside the unit
circle anyway for stability, this restriction is normally not binding
for the poles. However, zeros outside the unit circle--so-called
``non-minimum-phase zeros''--are used quite often in practice.
For a zero (or pole) outside the unit circle, we may rewrite the corresponding term of Eq. (8.9) as
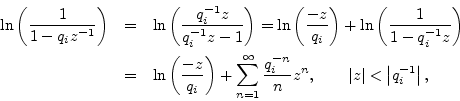
where we used a Maclaurin series expansion for
![]() once
again with the region of convergence including the unit circle. The
infinite sum in this expansion is now the bilateral z transform of an
anticausal sequence, i.e., one that is zero for nonnegative
times (
once
again with the region of convergence including the unit circle. The
infinite sum in this expansion is now the bilateral z transform of an
anticausal sequence, i.e., one that is zero for nonnegative
times (![]() ) and which decays in the direction of time
minus-infinity. The factored-out terms
) and which decays in the direction of time
minus-infinity. The factored-out terms ![]() and
and ![]() , for all
poles and zeros outside the unit circle, can be collected together and
associated with the overall gain factor
, for all
poles and zeros outside the unit circle, can be collected together and
associated with the overall gain factor ![]() in Eq. (8.9),
resulting in a modified scaling and time-shift for the original
sequence
in Eq. (8.9),
resulting in a modified scaling and time-shift for the original
sequence ![]() which can be dealt with separately
[60].
which can be dealt with separately
[60].
When all poles and zeros are inside the unit circle, the complex cepstrum is causal and can be expressed simply in terms of the filter poles and zeros as
![$\displaystyle {\tilde h}(n) = \left\{\begin{array}{ll}
\ln(g), & n=0 \\ [5pt]
\...
...ystyle\sum_{k=1}^M \frac{q_k^n}{n}, & n=1,2,3,\ldots\,, \\
\end{array}\right.
$](img1167.png)
In summary, each stable pole contributes a positive decaying
exponential (weighted by ![]() ) to the complex cepstrum, while each
zero inside the unit circle contributes a negative
weighted-exponential of the same type. The decaying exponentials
start at time 1 and have unit amplitude (ignoring the
) to the complex cepstrum, while each
zero inside the unit circle contributes a negative
weighted-exponential of the same type. The decaying exponentials
start at time 1 and have unit amplitude (ignoring the ![]() weighting)
in the sense that extrapolating them to time 0 (without the
weighting)
in the sense that extrapolating them to time 0 (without the ![]() weighting) would use the values
weighting) would use the values ![]() and
and
![]() . The
decay rates are faster when the poles and zeros are well inside the
unit circle, but cannot decay slower than
. The
decay rates are faster when the poles and zeros are well inside the
unit circle, but cannot decay slower than ![]() .
.
Poles and zeros outside the unit circle contribute anticausal exponentials to the complex cepstrum, negative for the poles and positive for the zeros.
As discussed in §12.4, any spectrum can be converted to minimum-phase form (without affecting the spectral magnitude) by computing its cepstrum and replacing any anticausal components with corresponding causal components. In other words, the anticausal part cepstrum, if any, is ``flipped'' about time zero so that it adds to the causal part. Doing this corresponds to reflecting non-minimum phase zeros (and any unstable poles) inside the unit circle in a manner that preserves spectral magnitude. The original spectral phase is then replaced by the unique minimum phase corresponding to the given spectral magnitude.
It can be remarked that each stable pole in the z transform gives rise to
a pole in the differentiated log ![]() -transform with residue
-transform with residue ![]() , while each
minimum-phase zero maps to a pole with residue
, while each
minimum-phase zero maps to a pole with residue ![]() .9.5
.9.5
For more about the cepstrum and the so-called Hilbert transform relations which relate the real and imaginary parts of the spectra of causal signals (which includes the phase and log-magnitude of minimum-phase spectra as a special case), see [60]. A matlab listing for computing a minimum-phase spectrum from the magnitude spectrum is given in §H.11.