In practice, we must work with a sampled frequency axis. That
is, instead of evaluating the transfer function
![]() at
at
![]() to obtain the frequency response
to obtain the frequency response
![]() , where
, where ![]() is continuous radian frequency, we compute instead
is continuous radian frequency, we compute instead
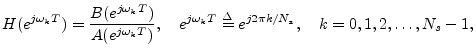
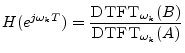
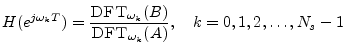

To avoid undersampling
![]() , we must have
, we must have ![]() , and to
avoid undersampling
, and to
avoid undersampling
![]() , we must have
, we must have ![]() . In general,
. In general,
![]() will be undersampled (when
will be undersampled (when ![]() ), because it is the
quotient of
), because it is the
quotient of
![]() over
over
![]() . This means, for example, that
computing the impulse response
. This means, for example, that
computing the impulse response ![]() from the sampled frequency
response
from the sampled frequency
response
![]() will be time aliased in general. I.e.,
will be time aliased in general. I.e.,
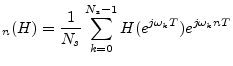
As is well known, when the DFT length ![]() is a power of 2, e.g.,
is a power of 2, e.g.,
![]() , the DFT can be computed extremely efficiently using
the fast Fourier transform (FFT). Figure 7.1 gives an
example matlab script for computing the frequency response of an IIR
digital filter using two FFTs. The Matlab function freqz
also uses this method when possible (i.e., when
, the DFT can be computed extremely efficiently using
the fast Fourier transform (FFT). Figure 7.1 gives an
example matlab script for computing the frequency response of an IIR
digital filter using two FFTs. The Matlab function freqz
also uses this method when possible (i.e., when ![]() is a power of 2).
is a power of 2).
function [H,w] = myfreqz(B,A,N,whole,fs) %MYFREQZ Frequency response of IIR filter B(z)/A(z). % N = number of uniform frequency-samples desired % H = returned frequency-response samples (length N) % w = frequency axis for H (length N) in radians/sec % Compatible with simple usages of FREQZ in Matlab. % FREQZ(B,A,N,whole) uses N points around the whole % unit circle, where 'whole' is any nonzero value. % If whole=0, points go from theta=0 to pi*(N-1)/N. % FREQZ(B,A,N,whole,fs) sets the assumed sampling % rate to fs Hz instead of the default value of 1. % If there are no output arguments, the amplitude and % phase responses are displayed. Poles cannot be % on the unit circle. A = A(:).'; na = length(A); % normalize to row vectors B = B(:).'; nb = length(B); if nargin < 3, N = 1024; end if nargin < 4, if isreal(b) & isreal(a), whole=0; else whole=1; end; end if nargin < 5, fs = 1; end Nf = 2*N; if whole, Nf = N; end w = (2*pi*fs*(0:Nf-1)/Nf)'; H = fft([B zeros(1,Nf-nb)]) ./ fft([A zeros(1,Nf-na)]); if whole==0, w = w(1:N); H = H(1:N); end if nargout==0 % Display frequency respone if fs==1, flab = 'Frequency (cyles/sample)'; else, flab = 'Frequency (Hz)'; end subplot(2,1,1); % In octave, labels go before plot: plot([0:N-1]*fs/N,20*log10(abs(H)),'-k'); grid('on'); xlabel(flab'); ylabel('Magnitude (dB)'); subplot(2,1,2); plot([0:N-1]*fs/N,angle(H),'-k'); grid('on'); xlabel(flab); ylabel('Phase'); end |