The most common type of filter dealt with in practice is a linear, causal, and time-invariant operator on the vector space consisting of arbitrary real-valued functions of time. Since we are dealing with the space of functions of time, we will use the terms vector, function, and signal interchangeably. When time is a continuous variable, the vector space is infinite-dimensional even when time is restricted to a finite interval. Digital filters are simpler in many ways theoretically because finite-time digital signals occupy a finite-dimensional vector space. Furthermore, every linear operator on the space of digital signals may be represented as a matrix.F.1If the range of time is restricted to N samples then the arbitrary linear operator is an N by N matrix. In the discussion that follows, we will be exclusively concerned with the digital domain. Every linear filter will be representable as a matrix, and every signal will be expressible as a column vector.
Linearity implies the superposition principle which is presently
indispensible for a general filter response analysis. The superposition
principle states that if a signal ![]() is represented as a linear
combination of signals
is represented as a linear
combination of signals
![]() , then the response
, then the response ![]() of any
linear filter
of any
linear filter ![]() may written as the same linear combination of the
signals
may written as the same linear combination of the
signals
![]() where
where ![]() . More generally,
. More generally,
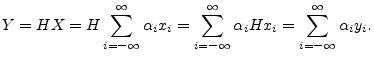
Causality means that the filter output does not depend on future inputs. This is necessary in analog filters where time is a real entity, but for digital filters causality is highly unnecessary unless the filter must operate in real-time. Requiring a filter to be causal results in a triangular matrix representation.
A time-invariant filter is one whose response does not depend on the
time of excitation. This allows superposition in time in
addition to the superposition of component functions given by
linearity. A matrix representing a linear time-invariant filter is
Toeplitz (each diagonal is constant). The chief value of
time-invariance is that it allows a linear filter to represented by
its impulse response which, for digital filters, is the response
elicited by the signal
![]() . A deeper consequence of
superposition in time together with superposition of component signal
responses is the fact that every stable linear time invariant filter
emits a sinusoid at frequency
. A deeper consequence of
superposition in time together with superposition of component signal
responses is the fact that every stable linear time invariant filter
emits a sinusoid at frequency ![]() in response to an input sinusoid at
frequency
in response to an input sinusoid at
frequency ![]() after sufficient time for start-up transients to
settle. For this reason sinusoids are called eigenfunctions of
linear time-invariant systems. Another way of putting it is that a
linear time-invariant filter can only modify a sinusoidal input by a
constant scaling of its amplitude and a constant offset in its phase.
This is the rationale behind Fourier analysis. The Laplace transform
of the impulse response gives the transfer function and the
Fourier transform of the impulse response is the frequency
response. It is important to note that relaxing time-invariance only
prevents us from using superposition in time. Consequently, while we
can no longer uniquely characterize a filter in terms of its impulse
response, we may still characterize it in terms of its basis
function response.
after sufficient time for start-up transients to
settle. For this reason sinusoids are called eigenfunctions of
linear time-invariant systems. Another way of putting it is that a
linear time-invariant filter can only modify a sinusoidal input by a
constant scaling of its amplitude and a constant offset in its phase.
This is the rationale behind Fourier analysis. The Laplace transform
of the impulse response gives the transfer function and the
Fourier transform of the impulse response is the frequency
response. It is important to note that relaxing time-invariance only
prevents us from using superposition in time. Consequently, while we
can no longer uniquely characterize a filter in terms of its impulse
response, we may still characterize it in terms of its basis
function response.
This will be developed below for the particular basis functions used in the Discrete Fourier Transform (DFT). These basis functions are defined for the N-dimensional discrete-time signal space as