Suppose we test the filter at each frequency separately. This is
called sine-wave analysis.2.1Fig.1.6 shows an example of
an input-output pair, for the filter of Eq. (1.1), at the
frequency ![]() Hz, where
Hz, where ![]() denotes the sampling rate. (The
continuous-time waveform has been drawn through the samples for
clarity.) Figure 1.6a shows the input signal, and Fig.1.6b
shows the output signal.
denotes the sampling rate. (The
continuous-time waveform has been drawn through the samples for
clarity.) Figure 1.6a shows the input signal, and Fig.1.6b
shows the output signal.
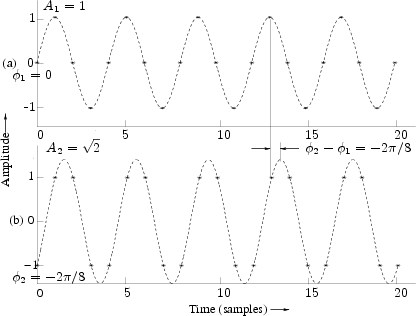 |
The ratio of the peak output amplitude to the peak input amplitude is
the filter gain at this frequency. From Fig.1.6 we find
that the gain is about 1.414 at the frequency ![]() . We may also
say the amplitude response is 1.414 at
. We may also
say the amplitude response is 1.414 at ![]() .
.
The phase of the output signal minus the phase of the input signal is
the phase response of the filter at this
frequency. Figure 1.6 shows that the filter of Eq. (1.1) has a
phase response equal to ![]() (minus one-eighth of a cycle) at the
frequency
(minus one-eighth of a cycle) at the
frequency ![]() .
.
Continuing in this way, we can input a sinusoid at each frequency
(from 0 to ![]() Hz), examine the input and output waveforms as in
Fig.1.6, and record on a graph the peak-amplitude ratio (gain)
and phase shift for each frequency. The resultant pair of plots, shown
in Fig.1.7, is called the frequency response. Note that
Fig.1.6 specifies the middle point of each graph in Fig.1.7.
Hz), examine the input and output waveforms as in
Fig.1.6, and record on a graph the peak-amplitude ratio (gain)
and phase shift for each frequency. The resultant pair of plots, shown
in Fig.1.7, is called the frequency response. Note that
Fig.1.6 specifies the middle point of each graph in Fig.1.7.
Not every black box has a frequency response, however. What good is a pair of graphs such as shown in Fig.1.7 if, for all input sinusoids, the output is 60 Hz hum? What if the output is not even a sinusoid? We will learn in Chapter 4 that the sine-wave analysis procedure for measuring frequency response is meaningful only if the filter is linear and time-invariant (LTI). Linearity means that the output due to a sum of input signals equals the sum of outputs due to each signal alone. Time-invariance means that the filter does not change over time. We will elaborate on these technical terms and their implications later. For now, just remember that LTI filters are guaranteed to produce a sinusoid in response to a sinusoid--and at the same frequency.