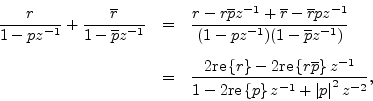
Implementing the partial fraction expansion (§6.8.7) directly results in a set of parallel complex resonators for the IIR part. The same result is obtained by implementing a diagonalized state-space model (Eq. (E.22)). In practice, however, signals are typically real-valued functions of time. As a result, for real filters,10.5it is typically more economical to combine complex-conjugate one-pole sections together to form real second-order sections (two poles, one zero, in general). This process was discussed in §6.8.1, and the resulting transfer function of each second-order section becomes
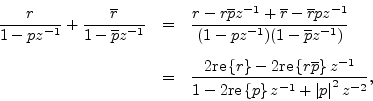
where ![]() is one of the poles, and
is one of the poles, and ![]() is its corresponding residue.
Figure 3.21 and Fig.3.22 illustrates a filter realization consisting
of one first-order, and two second-order
parallel filter sections.
is its corresponding residue.
Figure 3.21 and Fig.3.22 illustrates a filter realization consisting
of one first-order, and two second-order
parallel filter sections.
Finally, Fig.9.5 illustrates an efficient implementation of terms due to a repeated pole with multiplicity three, contributing the additive terms