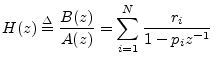 |
(7.7) |
An important tool for inverting the z transform and converting among digital filter implementation structures is the partial fraction expansion (PFE). The term ``partial fraction expansion'' refers to the expansion of a rational transfer function into a sum of first and/or second-order terms. The case of first-order terms is the simplest and most fundamental:

and ![]() . (The case
. (The case ![]() is addressed in the next section.)
The denominator coefficients
is addressed in the next section.)
The denominator coefficients ![]() are called the poles of the
transfer function, and each numerators
are called the poles of the
transfer function, and each numerators ![]() is called the
residue of pole
is called the
residue of pole ![]() . Equation (6.7) is general only if the poles
. Equation (6.7) is general only if the poles
![]() are distinct. (Repeated poles are addressed in
§6.8.5 below.) Both the poles and their residues may be complex.
The poles may be found by factoring the polynomial
are distinct. (Repeated poles are addressed in
§6.8.5 below.) Both the poles and their residues may be complex.
The poles may be found by factoring the polynomial ![]() into
first-order terms,7.2 e.g.,
using the roots function in matlab.
The residue
into
first-order terms,7.2 e.g.,
using the roots function in matlab.
The residue ![]() corresponding to pole
corresponding to pole ![]() may be found
analytically as
may be found
analytically as
Note that in Eq. (6.8), there is always a pole-zero cancellation at
![]() . That is, the term
. That is, the term
![]() is always cancelled by an
identical term in the denominator of
is always cancelled by an
identical term in the denominator of ![]() , which must exist because
, which must exist because
![]() has a pole at
has a pole at ![]() . The residue
. The residue ![]() is simply the
coefficient of the one-pole term
is simply the
coefficient of the one-pole term
![]() in the partial
fraction expansion of
in the partial
fraction expansion of ![]() at
at ![]() . The transfer function
is
. The transfer function
is
![]() , in the limit, as
, in the limit, as ![]() .
.